SVM - NIT tutorial (part 17)

Using Support Vector Machines (SVM) to build the model
R
NIT Tutorial
SVM
Author

José Ramón Cuesta

Published

March 28, 2023

Let´s load first the previous workspace and the libraries needed.

load("C:/BLOG/Workspaces/NIT Tutorial/NIT_ws16.RData")
library(tidyverse)
library(caret)
library(earth)
library(Monitor)

We all have listen about Support Vector Machines algorithm to build Chemometric models, but I never try to do it , so this tutorial is a good opportunity to try. I use Caret package and use a default procedure described in the book “Applied Predictive Modeling”, so we know that there is margin for improvement with other configurations.

As always we develop the model with the samples selected for training and validate eith the samples taken apart for testing.

SVM model for Protein

set.seed(100)
svm_tec_prot <- train(x = tec2_prot_train$snvdt2der2_spec, y = tec2_prot_train$Protein, 
                       method = "svmRadial",
                       tuneLength = 14,
                       preproc = c("center", "scale"),
                       trControl = trainControl(method = "cv"))
svm_protpreds <- predict(svm_tec_prot, tec2_prot_test$snvdt2der2_spec)
test_prot_svmpreds <- bind_cols(tec2_prot_test$SampleID ,tec2_prot_test$Protein, svm_protpreds)
colnames(test_prot_svmpreds) <- c("SampleID", "Prot_lab", "Prot_pred")

test_prot_svmpreds %>% 
ggplot( aes(x = Prot_pred, y = Prot_lab)) + 
  geom_point()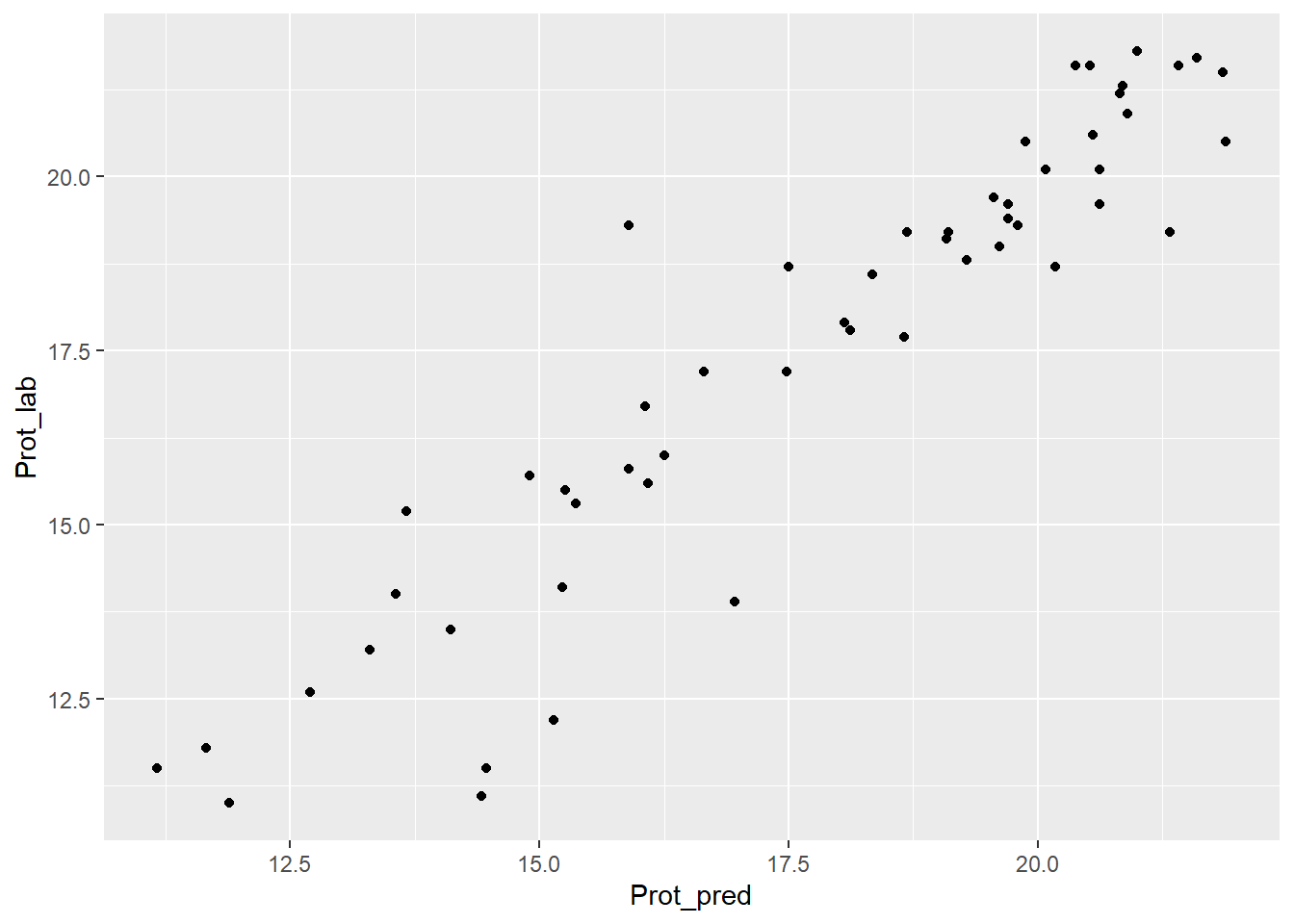

Let´s use the Monitor package to see the statistics:

monitor_xyplot(test_prot_svmpreds[ , 1:3])
Validation Samples  = 55 
Reference Mean      = 17.59455 
Predicted Mean      = 17.79309 
RMSEP               : 1.16366 
Bias                : -0.1985454 
SEP                 : 1.157165 
Corr                : 0.9356546 
RSQ                 : 0.8754495 
Slope               : 1.022215 
Intercept           : -0.5938104 
*** Std Dev of the model not supplied, RPD not calculated ***
*** Details of the model used for prediction not supplied ***
***      SEP significance not calculated                  ***
Residual Std Dev is : 1.17 
    ***Slope/Intercept adjustment in not necessary***
Bias                : -0.1985454 
SEP                 : 1.157165 
BCL(+/-)            : 0.3126953 
BCL percentage: 31.26953 
***Bias adjustment in not necessary***
Without any adjustment and using  SEP as std dev the residual distibution is: 
  Residuals into 68%   prob (+/- 1SEP)    = 44     % = 80 
  Residuals into 95%   prob (+/- 2SEP)    = 50     % = 90.90909 
  Residuals into 99.5% prob (+/- 3SEP)    = 55     % = 100 
  Residuals outside 99.5% prob (+/- 3SEP) = 0      % = 0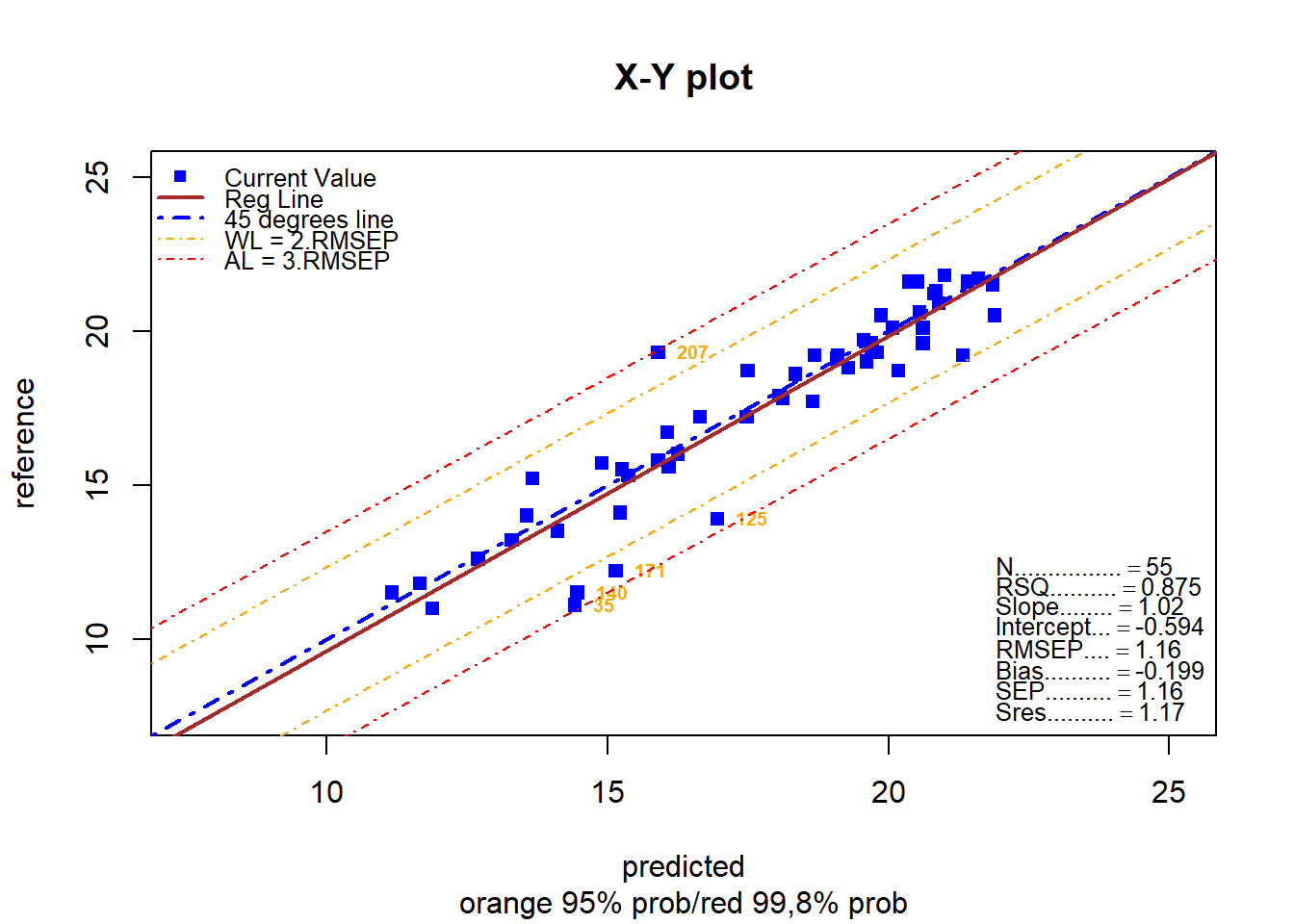 

$ResWarning
   index  id  ref     pred       res res.corr1 res.corr2          Q   Color
12    12  35 11.1 14.42107 -3.321071     -3.12     -3.05 Q1 to MIN  #0000FF
36    36 125 13.9 16.95782 -3.057816     -2.86     -2.84 Q1 to MIN  #0000FF
39    39 140 11.5 14.46377 -2.963773     -2.77     -2.69 Q1 to MIN  #0000FF
47    47 171 12.2 15.14471 -2.944707     -2.75     -2.69 Q1 to MIN  #0000FF
55    55 207 19.3 15.89985  3.400155      3.60      3.64         Q2 #FFFF33

$ResWarningList
[1] 12 36 39 47 55

$ResAction
[1] index     id        ref       pred      res       res.corr1 res.corr2
[8] Q         Color    
<0 rows> (or 0-length row.names)

$ResActionList
numeric(0)

SVM model for Fat

set.seed(100)
svm_tec_fat <- train(x = tec2_prot_train$snvdt2der2_spec, y = tec2_prot_train$Fat, 
                       method = "svmRadial",
                       tuneLength = 14,
                       preproc = c("center", "scale"),
                       trControl = trainControl(method = "cv"))
svm_fatpreds <- predict(svm_tec_fat, tec2_fat_test$snvdt2der2_spec)
test_fat_svmpreds <- bind_cols(tec2_fat_test$SampleID ,tec2_fat_test$Fat, svm_fatpreds)
colnames(test_fat_svmpreds) <- c("SampleID", "Fat_lab", "Fat_pred")

test_fat_svmpreds %>% 
ggplot( aes(x = Fat_pred, y = Fat_lab)) + 
  geom_point()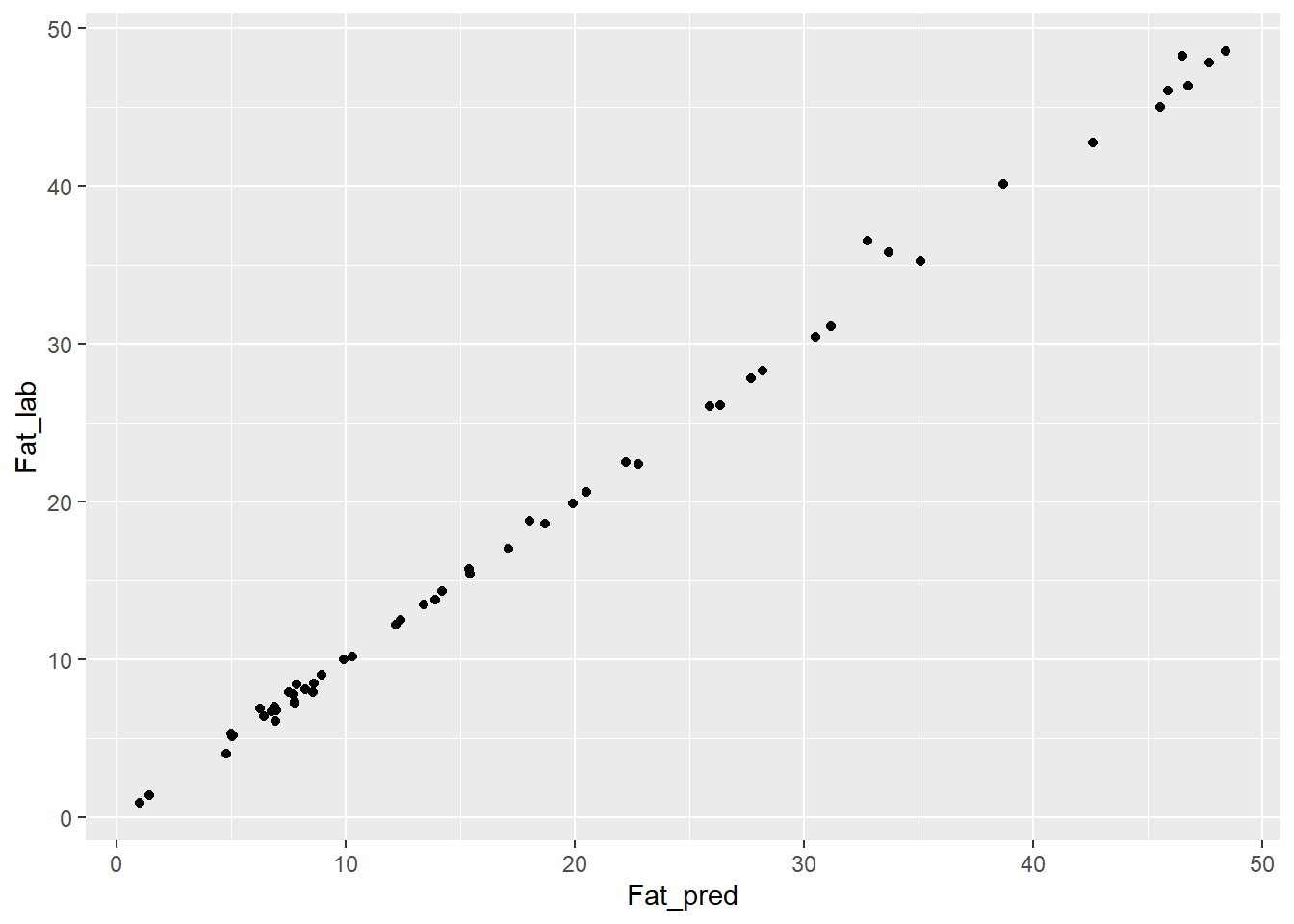

Let´s use the Monitor package to see the statistics:

monitor_xyplot(test_fat_svmpreds[ , 1:3])
Validation Samples  = 55 
Reference Mean      = 19.01091 
Predicted Mean      = 18.87002 
RMSEP               : 0.7133293 
Bias                : 0.1408927 
SEP                 : 0.7057218 
Corr                : 0.9988758 
RSQ                 : 0.9977529 
Slope               : 1.014583 
Intercept           : -0.1342866 
*** Std Dev of the model not supplied, RPD not calculated ***
*** Details of the model used for prediction not supplied ***
***      SEP significance not calculated                  ***
Residual Std Dev is : 0.68 
    ***Slope/Intercept adjustment is recommended***
Bias                : 0.1408927 
SEP                 : 0.7057218 
BCL(+/-)            : 0.1907039 
BCL percentage: 19.07039 
***Bias adjustment in not necessary***
Without any adjustment and using  SEP as std dev the residual distibution is: 
  Residuals into 68%   prob (+/- 1SEP)    = 48     % = 87.27273 
  Residuals into 95%   prob (+/- 2SEP)    = 52     % = 94.54545 
  Residuals into 99.5% prob (+/- 3SEP)    = 54     % = 98.18182 
  Residuals outside 99.5% prob (+/- 3SEP) = 1      % = 1.818182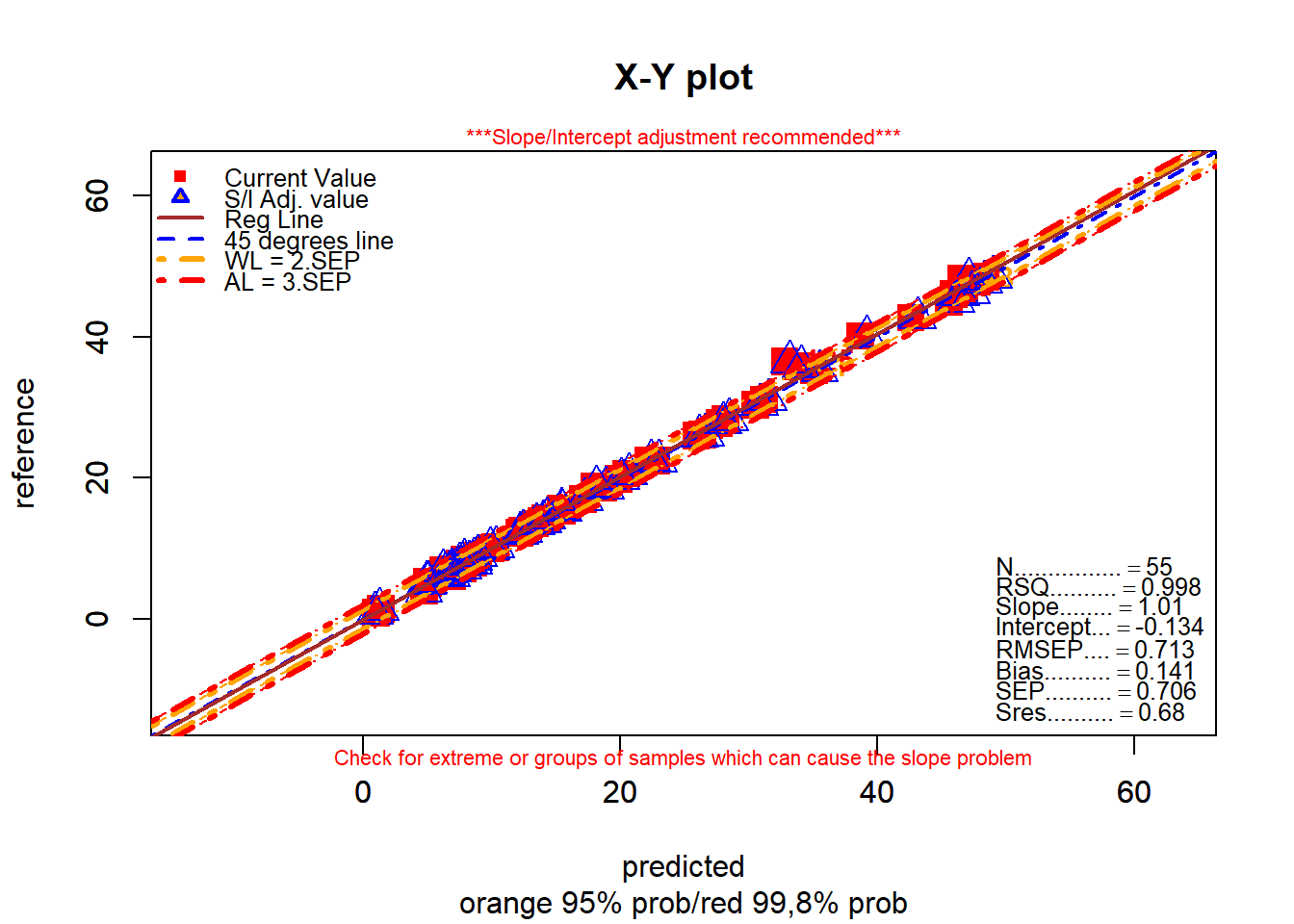 

With S/I correction and using Sres as standard deviation, the Residual Distribution would be:
  Residuals into 68%   prob (+/- 1Sres)     = 47     % = 85.45455 
  Residuals into 95%   prob (+/- 2Sres)     = 53     % = 96.36364 
  Residuals into 99.5% prob (+/- 3Sres)     = 54    % = 98.18182 
  Residuals outside  99.5% prob (> 3Sres)   = 1     % = 1.818182 
$ResWarning
   index id  ref     pred      res res.corr1 res.corr2         Q   Color
13    13 41 35.8 33.69096 2.109041      1.97      1.75 Q2 to MAX #FF9933
14    14 43 48.2 46.52586 1.674137      1.53      1.13 Q2 to MAX #FF9933

$ResWarningList
[1] 13 14

$ResAction
   index  id  ref     pred      res res.corr1 res.corr2         Q   Color
33    33 125 36.5 32.79654 3.703458      3.56      3.36 Q2 to MAX #FF9933

$ResActionList
[1] 33

SVM model for Moisture

set.seed(100)
svm_tec_moi <- train(x = tec2_moi_train$snvdt2der2_spec, y = tec2_moi_train$Moisture, 
                       method = "svmRadial",
                       tuneLength = 14,
                       preproc = c("center", "scale"),
                       trControl = trainControl(method = "cv"))
svm_moipreds <- predict(svm_tec_moi, tec2_moi_test$snvdt2der2_spec)
test_moi_svmpreds <- bind_cols(tec2_moi_test$SampleID ,tec2_moi_test$Moisture, svm_moipreds)
colnames(test_moi_svmpreds) <- c("SampleID", "Moisture_lab", "Moisture_pred")

test_moi_svmpreds %>% 
ggplot( aes(x = Moisture_pred, y = Moisture_lab)) + 
  geom_point()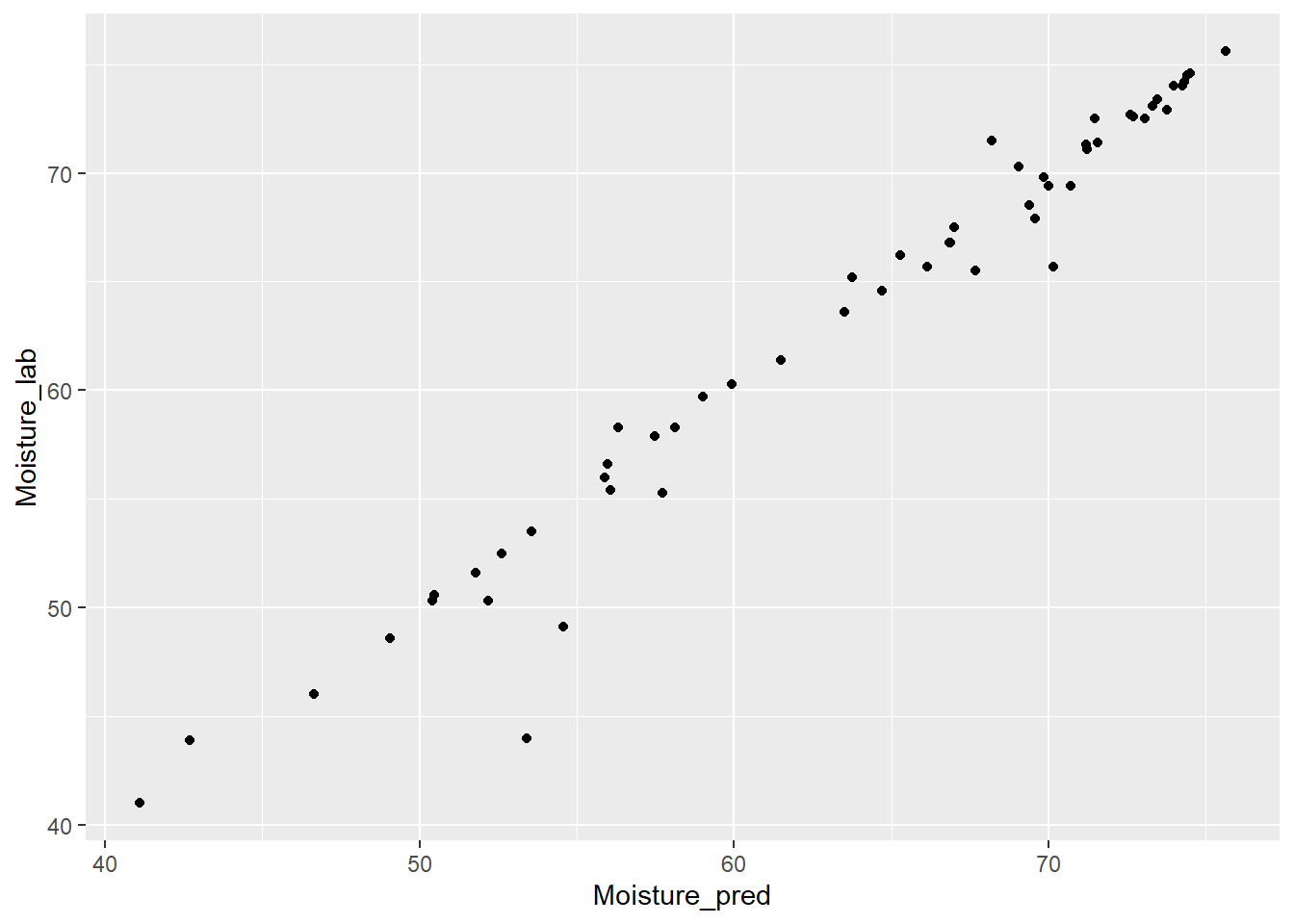

Let´s use the Monitor package to see the statistics:

monitor_xyplot(test_moi_svmpreds[ , 1:3])
Validation Samples  = 56 
Reference Mean      = 63.3625 
Predicted Mean      = 63.75773 
RMSEP               : 1.815258 
Bias                : -0.3952311 
SEP                 : 1.787743 
Corr                : 0.9830242 
RSQ                 : 0.9663366 
Slope               : 1.020187 
Intercept           : -1.682337 
*** Std Dev of the model not supplied, RPD not calculated ***
*** Details of the model used for prediction not supplied ***
***      SEP significance not calculated                  ***
Residual Std Dev is : 1.79 
    ***Slope/Intercept adjustment in not necessary***
Bias                : -0.3952311 
SEP                 : 1.787743 
BCL(+/-)            : 0.4785686 
BCL percentage: 47.85686 
***Bias adjustment in not necessary***
Without any adjustment and using  SEP as std dev the residual distibution is: 
  Residuals into 68%   prob (+/- 1SEP)    = 48     % = 85.71429 
  Residuals into 95%   prob (+/- 2SEP)    = 53     % = 94.64286 
  Residuals into 99.5% prob (+/- 3SEP)    = 54     % = 96.42857 
  Residuals outside 99.5% prob (+/- 3SEP) = 2      % = 3.571429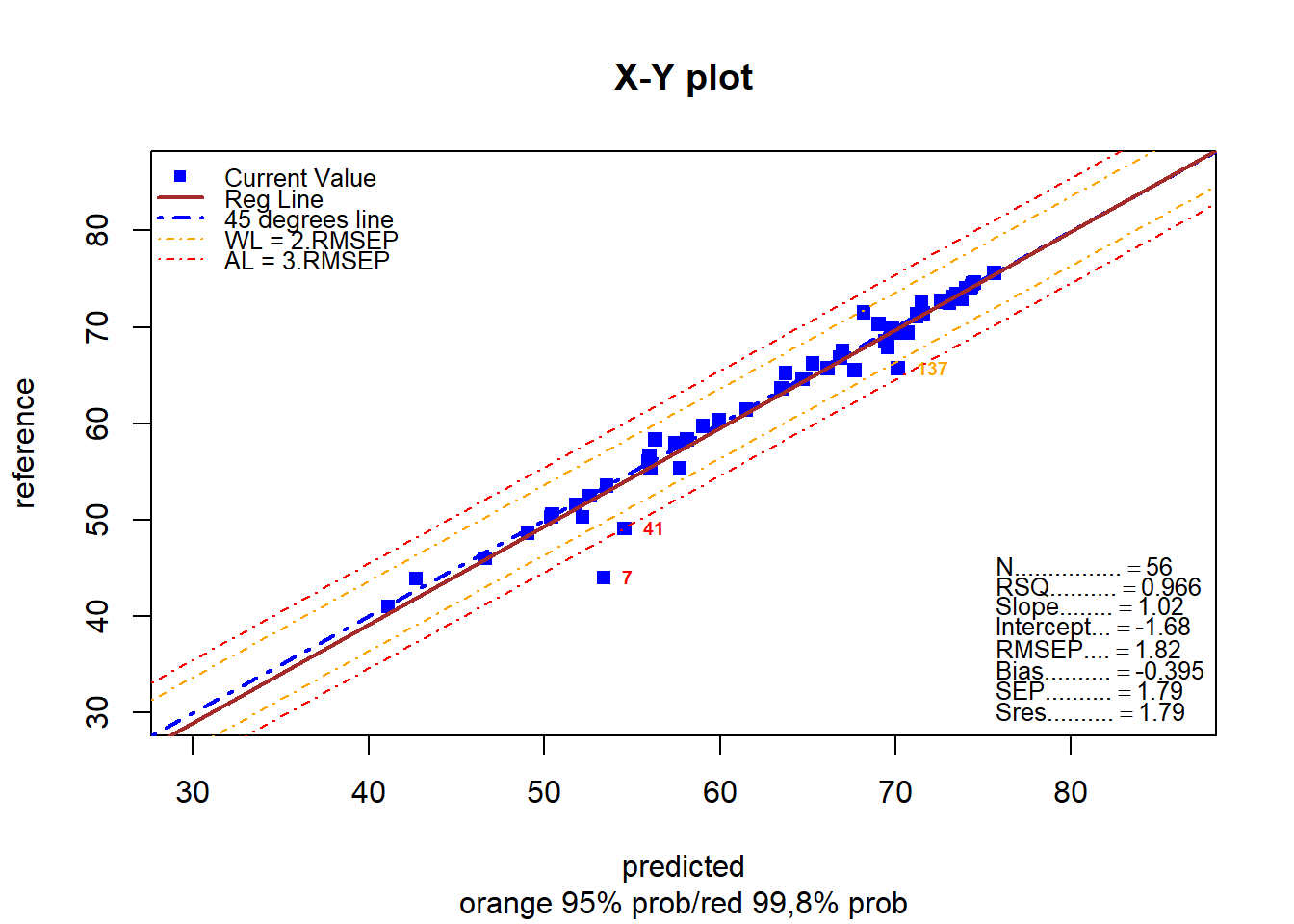 

$ResWarning
   index  id  ref     pred       res res.corr1 res.corr2  Q   Color
38    38 137 65.7 70.14363 -4.443631     -4.05     -4.18 Q1 #00CC66

$ResWarningList
[1] 38

$ResAction
   index id  ref     pred       res res.corr1 res.corr2          Q   Color
3      3  7 44.0 53.40620 -9.406203     -9.01     -8.80 Q1 to MIN  #0000FF
17    17 41 49.1 54.57022 -5.470218     -5.07     -4.89 Q1 to MIN  #0000FF

$ResActionList
[1]  3 17

As we can see the statistics are quite good for all the parameters (specially for fat and moisture), and show us that this algorithm must be considered when developing NIR models.